Opinión | Cometamos nuevos Errores: por qué las gráficas de líneas deben comenzar en cero

De "pienso y entiendo" a "miro y entiendo"

Una gráfica es la representación de relaciones entre datos numéricos por medio de un dibujo. Desde el punto de vista de la Usabilidad, podemos decir que una gráfica transforma un problema "pienso y entiendo" en un problema "miro y entiendo".

Esta definición nos ayuda mucho a entender qué atributos debe tener una gráfica para poder ser realmente una gráfica: la persona que se enfrenta a ella tiene que entender con solo mirar algo equivalente a lo que hubiera entendido pensando a partir de los datos que le dan soporte. Y por el contrario, si al mirar el dibujo entiende algo distinto a lo que entendería analizando los números, la gráfica está mal.

Como corolario podemos afirmar que si para entender correctamente es necesario acudir a los datos, la gráfica está mal porque vuelve a transformar el problema en "pienso y entiendo". Y esto incluye las etiquetas del eje vertical, el eje de las Y. Quien se enfrenta a una gráfica sabe que alcanza con mirar para entender, y no resulta natural ni lógico que sea obligatorio tomar en cuenta algún dato numérico para entender.

Gráficas complejas

El mundo de las gráficas es amplio y diverso y abarca un enorme espectro de posibilidades, que incluyen gráficas mucho más complejas que las de barras o líneas. Existe abundante literatura al respecto, de excelente calidad, donde podemos tomar como eje de referencia el libro de Edward Tufte "The visual display of cuantitative information" (La visualización de información cuantitativa) o la obra maestra de Darrell Huff "How to lie with statistics" (Como mentir con estadísticas)

En términos generales podemos decir que una gráfica es compleja cuando para entenderla es necesario contar con información complementaria a la que se incluye de forma visual.

El significado de los colores, del grosor de las líneas, o de la forma de los puntos son algunos ejemplos característicos de este tipo de información adicional.

Para que pueda ser considerado una gráfica se deben tomar en cuenta al menos dos condiciones sine qua non:

- La información adicional no puede ser la propia información numérica que se intenta representar.
- El nivel "miro y entiendo" no puede transmitir una idea errónea de los datos.

Este último punto es muy relevante. Por más complejo que sea la gráfica y por más elementos adicionales que se requieran, en ningún caso es aceptable que transmita a quien no cuenta con la información adicional una idea errónea de los datos que representa. Tal vez quien la mira por primera vez no entienda la información, o la entienda parcialmente, pero jamás debería entender otra cosa si no conoce los datos adicionales.

As seen in TV

Las gráficas que generalmente se muestran en los medios, y que constituyen el objeto de esta nota, son habitualmente muy elementales: gráficas de líneas o de barras que representan una única serie numérica que evoluciona a lo largo del tiempo.

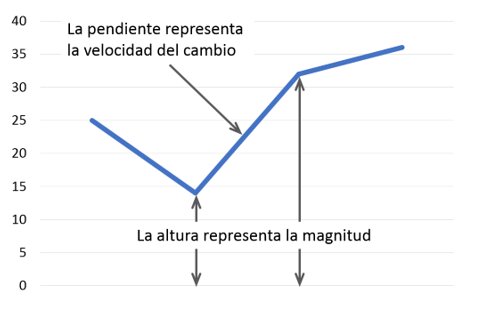
Se trata de un gráfico simple y archiconocido: La altura de la barra o del punto representa la magnitud de la serie numérica en la fecha dada, y la pendiente de la línea que va entre dos puntos la velocidad del cambio.

En la simplicidad radica su elegancia y su potencia: explota la extrema habilidad de nuestra visión para comparar magnitudes lineales que se encuentran una junto a la otra, sumado al largo entrenamiento que proporciona haber visto miles de gráficas similares, transformando el tiempo considerable que requeriría analizar una serie numérica en un instante.

Cuando una gráfica de líneas (o barras) no comienza en cero

Cuando en una de estas gráficas de líneas utilizadas de forma ubicua en los medios el eje de las Y no comienza en cero, quien lo mira entiende algo distinto a lo que entendería viendo la serie numérica y por tanto están mal. Las alturas no representan más la magnitud del dato y la pendiente no es proporcional a la velocidad de cambio.

El argumento de que "se entiende mirando los datos del eje de las Y" no es de recibo, en primer lugar, porque viola flagrantemente la noción misma de gráfica: el nivel "miro y entiendo" transmite un concepto distinto del nivel "pienso y entiendo".

Aceptar que el eje vertical puede comenzar en cualquier valor, supone dejar abierto completamente lo que se entenderá al mirarla, y por tanto permite transmitir una interpretación distinta a la que se deduce de los datos numéricos. Si esto es por omisión o ignorancia, se trata de un error. Si es deliberado, se trata de una mentira.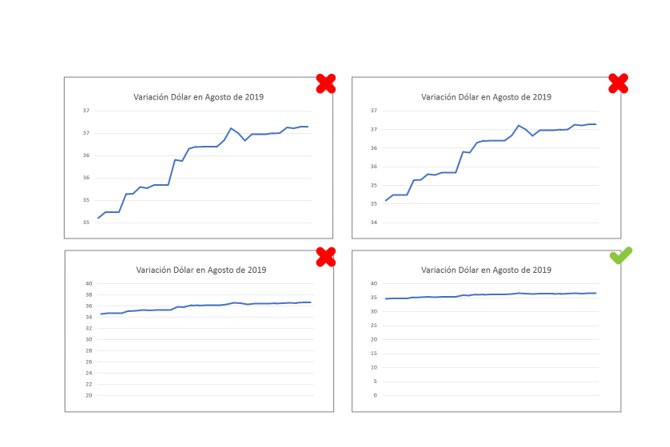

Por supuesto que muchas veces al obligar a la gráfica a comenzar el eje de las Y en cero deja de transmitir lo que quien la muestra quiere representar. Por ejemplo, si durante 6 meses el dólar varió de a centésimos y de pronto empieza a variar en pesos, la gráfica del valor del dólar seguramente no lo va a mostrar.

En ese caso lo que hay que hacer es otra gráfica, y no intentar forzar al gráfica original. En vez de graficar el valor, graficar la magnitud del cambio, o cualquier otra magnitud que represente exactamente lo que queremos. Es cierto que esto requiere que quien hace la gráfica sea algo más que un chofer de mouse.

Si todavía no te convenciste

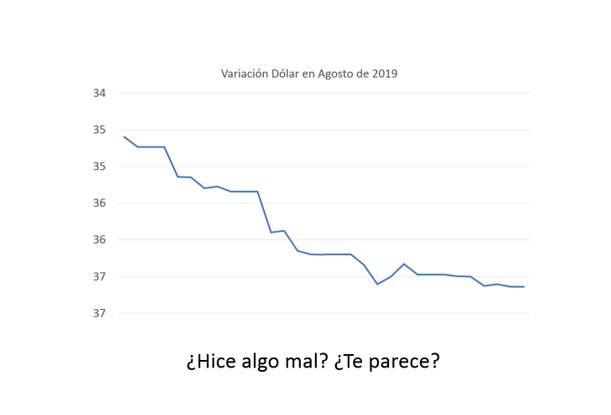
Si todos estos argumentos no ten convencieron aún, y seguís creyendo que "se puede ajustar el eje vertical para mostrar lo que uno necesita", entonces tendrás que aceptar que la gráfica de más abajo es completamente válida, ¿O no?